统计学中矩的理解
概述
矩(moment)在统计学中用的很多,我们对他可能只有公式上的印象,但是他到底代表什么 总是不明白。
最初我们认识矩这个概念,主要是因为物理学里面力矩而来( \(M=FL\) )。如下图:
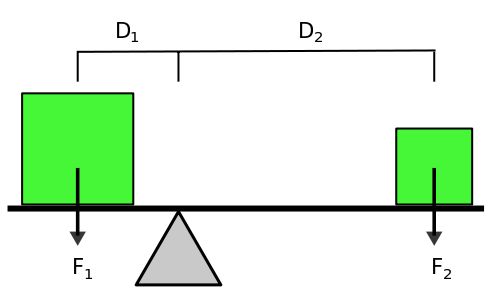
Figure 1: 力矩
在这里,对于固定的支点,两个不同重量的物体,他们摆放在一定的位置才能确保相对支 点的平衡,也就是 \(F_1D_1 = F_2D_2\) 。我们把力和距离支点的距离乘积叫做力矩,当两 者相对同一个支点的力矩相等时(当然方向要相反),他们就能够平衡。值得注意的是,力 矩中的距离必须是与力的方向垂直的方向。
所以理解起来,矩和一个相对点有关系,而且可以通过矩来衡量一种相对某个点的平衡关 系。现在我们固定矩这个量,来讨论另外两个影响因素,\(M=FL\) ,当矩固定的时候,力F和 距离支点的距离L成反比。如果要达到相同的矩,那么F越大,就要求距离支点的距离L越 小,反之,F越小,距离L就要越大。也就是说当F越小的时候,作用点偏离支点的距离的 程度就越大。
上面这种情况我们忽略了平衡杆的质量,因为一根空杆其实是用重力作用的,如果我们把 一个杆均分成n等份,那么越靠近支点的地方力矩越小,越远力矩就越大,整个杆的力矩 可以使用积分(或者等份累加)起来,这样力矩的计算就是所有质量块与距离乘积的和:
\begin{equation} M=\sum_{i=1}^{n}m_il_i \end{equation}这个公式看起来会很眼熟,后面会看到类似的公式。
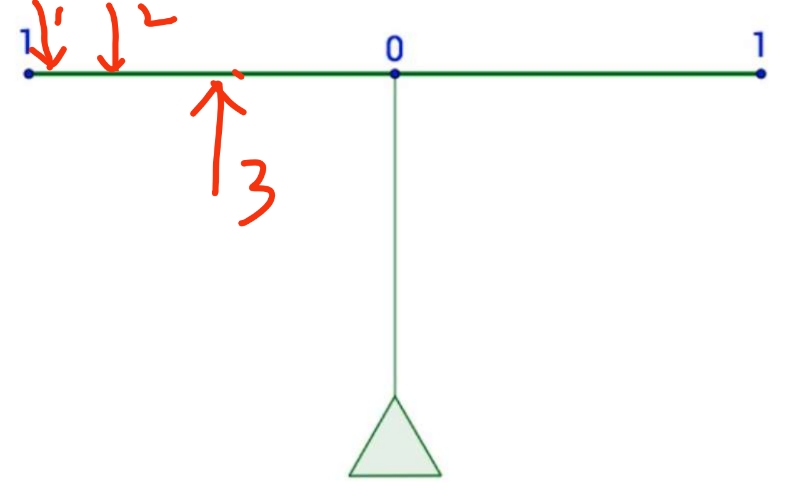
Figure 2: 表示能量的矩
现在我们再考虑一种情况,有三个作用力 \(F_1\) , \(F_2\) , \(F_3\) 。其中两个方向向下, 另一个向上,我们要衡量三个力的总的能量,怎么办呢?将其取平方:
\begin{equation} E_m=\sum_{i=1}^{n}(m_il_i)^{2} \end{equation}现在我们看看统计学里面的矩如何理解呢?
统计学中的矩
考虑福利彩票的粒子:每一注2元,中奖几率:
| 奖金额度/元 | 中奖概率 |
|---|---|
| 5 | 10% |
| 100 | 0.5% |
| 5000000 | 0.00001% |
等于0.5元代表的:
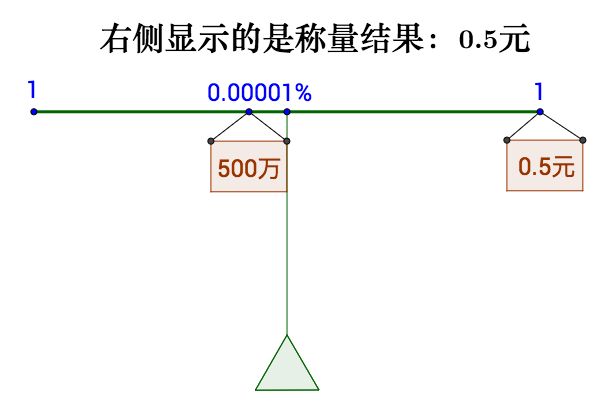
Figure 3: 福利彩票
那可以理解为不确定的500w等价与确定的0.5元。同样三个奖项的矩计算出来是(这样相当 于这张彩票才值1.5元,小于购买价格2元,购买者实际是亏的):
5 X 10% + 100 X 0.5% + 5000000 X 0.00001% = 1.5
如果我们把 \(x_i\) 表示奖金金额,\(p_i\) 表示获得该金额的概率。那么上面的矩表示公 式就是:
\begin{equation} E(X)=\sum_{i=1}^{n}p_ix_i \end{equation}考虑一种情况,如果发生概率相同,那么该公式就变成了:
\begin{equation} E(X)=\frac{1}{n}\sum_{i=1}^{n}x_i \end{equation}这两种形式其实代表的是平均值。
这个公式大家很熟悉吧,就是统计学里面的期望。这个公式和上面计算力矩的公式形式是 一样的。分析这个公式,当我们采集一定适量的样本之后,可以通过这个公式计算他们的 期望,这个期望实际就描述了这些样本分布的属性。当期望固定之后,我们就可以估算对 应的采样值的采样概率了。但实际上,仅仅使用期望还无法估计某个采样的分布,我们还 需要更多的信息。和上面一样,我们也可以定义表示能量的平方形式:
\begin{equation} E_m(X)=\sum_{i=1}^{n}(p_ix_i)^2 \end{equation}如果发生概率相同,那么该公式就变成了:
\begin{equation} E(X)=\frac{1}{n}\sum_{i=1}^{n}(x_i)^2 \end{equation}这两种形式其实代表的是平均能量。
现在我们直接引入矩的概念,然后再讨论用来表示分布的更多信息。
矩的概念
如果用下面这个图来表示,我们把支点看做是原点,那么上面的矩就是相对原点的矩,即 原点矩。我们还可以选择其他有代表性的点作为支点,那就还有相对其他点的矩,比如, 我们求出均值之后,相对均值的矩称为中心距。同时取平方的我们叫二阶矩,三次方的叫 三阶矩。总结如下:
| 名称 | 表示形式 | 含义 |
|---|---|---|
| 样本矩 | \(\frac{1}{n}\sum_{i=1}^{n}x_i\) | 近似估计,假设所有情况概率相同。 |
| 一阶原点矩/期望 | \(\sum_{i=1}^{n}p_ix_i\) | 也称为随机变量的中心,加权均值。 |
| 二阶原点矩 | \(\sum_{i=1}^{n}(p_ix_i)^2\) | |
| 一阶中心距 | \(\sum_{i=1}^{n}p_i(x_i-\mu)\) | 显然,任何随机变量的一阶中心距都是0。 |
| 二阶中心距/方差 | \(\sum_{i=1}^{n}p_i(x_i-\mu)^2\) | 表示该变量离其期望值的离散程度(距离)。平方根叫标准差。 |
| 三阶中心距/偏态 | \(\sum_{i=1}^{n}p_i(x_i-\mu)^3\) | 偏度衡量实数随机变量概率分布的不对称性。 |
| 四阶中心距/峰态 | \(\sum_{i=1}^{n}p_i(x_i-\mu)^4\) | 峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。 |
下面说明一下这几个概念表达的意思:
- 期望(Expectation): 表示加权平均。
- 方差(Variance): 表示某个样本或变量偏离期望值的程度或者距离。
- 偏态(Skewness): 在概率论和统计学中,偏度衡量实数随机变量概率分布的不对称性。偏度的值可 以为正, 可以为负或者甚至是无法定义。在数量上,偏度为负(负偏态)就意味着在概 率密度函数 左侧的尾部比右侧的长,绝大多数的值(不一定包括中位数在内)位于 平均值的右侧。偏 度为正(正偏态)就意味着在概率密度函数右侧的尾部比左侧的长,绝大多数的值(不一定 包括中位数)位于平均值的左侧。偏度为零就表示数值相对均匀地分布在平均值的两侧,但 不一定意味着其为对称分布。
- 峰态(Kurtosis): 在统计学中,峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。